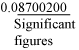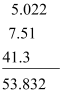3 Uncertainty in Measurement
Uncertainty in Measurement
Scientific Notation
- Exponential notation in which a number can be represented in the form N × 10n, where n = positive; N varies between 1 and 10.
| Example
Express the following in the scientific notation. (i) 0.00502 (ii) 32010.07 Solution: (i) 5.02 × 10−3 (ii) 3.201007 × 104 |
- Multiplication and division
(1.7 × 10−7) × (5.9 × 102) = (1.7 × 5.9) (10 − 7 + 2)
= (1.7 × 5.9) × 10−5
= 10.03 × 10−5
= 1.003 × 10−4
- Addition and subtraction
- The numbers are written by keeping the exponent same.
Example:
7.25 × 10−3 + 4.12 × 10−5
= 7.25 × 10−3 + 0.0412 × 10−3
= (7.25 + 0.0412) × 10−3
= 7.2912 × 10−3
Example:
2.87 × 107 − 5.1 × 106
= 2.87 × 107 − 0.51 × 107
= (2.87 − 0.51) × 107
= 2.36 × 107
Significant Figures
| Precision | Accuracy |
| Closeness of various measurements for the same quantity | Agreement of a particular value to the true value of the result |
| Expressed as the difference between a measured value and the arithmetic mean value for a series of measurements
i.e., Precision = Individual value − Arithmetic mean value |
Expressed as the difference between the experimental value or the mean value of a set of measurements and the true value
i.e., Accuracy = Mean value − True value |
- Comprise meaningful digits which are known with certainty
- Indicated by writing the certain digits and the last uncertain digit
- Example, in a result 45.8 cm, 45 is certain and 8 is uncertain. The uncertainty would be ± 1 in the last digit.
- If not stated, then the uncertainty in the last digit is understood as ± 1.
- Rules to determine the number of significant figures:
- All non-zero digits are significant. Example: 145 mL has three significant figures.
- Zeroes preceding the first non-zero digit are not significant. Example: 0.04281 has four significant figures.
- Zeroes between two non-zero digits are significant. Example: 23.007 has five significant figures.
- Zeroes at the end or right of a number are significant when they are on the right side of the decimal point. Example: 0.8300 has four significant figures.
- Counting numbers of objects have infinite significant figures as these are exact numbers and can be represented by writing infinite number of zeros after placing a decimal. Example: 25 books can be represented as 25 = 25.00000000
| Example
How many significant figures are present in 0.08700200? Solution There are seven significant figures. |
- Addition and subtraction of significant figures:
- The result must not have more digits to the right of the decimal point than either of the original numbers.
- Example:
Since 41.3 has only one digit to the right of the decimal point, the result will be 53.8.
- Multiplication and division of significant figures.
- The result must not have more significant figures than that of the original numbers with the few significant figures.
- Example: 1.1 × 2.134 = 2.3474
Since 1.1 has two significant figures, the result will be 2.3.
- Rules for rounding off numbers:
- If greater than 5, then increased by 1
- If less than 5, then not changed
- If equal to 5, then increased by 1 (in case of odd number) and not changed (in case of even number)
Dimensional Analysis
- Method used to convert units from one system to other − Factor label method or unit factor method or dimensional analysis
| Example
Calculate the volume of 3.5 L water in m3. Solution We know that 1 L = 1000 cm3 = (10 cm)3 Since 100 cm = 1 m, 10 cm = 0.1 m Now, 1 L = (10 cm)3 = (0.1 m)3 = (1 × 10−1 m)3 = 1 × 10−3 m3 Therefore, 3.5 L = 3.5 × 1 × 10− 3 m3 = 3.5 × 10−3 m3 |