5 Colligative Properties and Determination of Molar mass

• Properties which depend upon the number of solute particles present in the solution irrespective of their nature, relative to the total number of particles present in the solution
• Examples: Relative lowering of vapour pressure of the solvent, depression of freezing point of the solvent, elevation of boiling point of the solvent, osmotic pressure of the solution

Relative Lowering of Vapour Pressure

• Relative lowering of vapour pressure is equal to the mole fraction of the solute.

i.e.,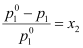

Where,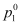= Vapour pressure of the solvent

   p₁ = Vapour pressure of the solution

  x₂ = Mole fraction of the solute

However,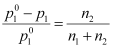

Where, n₂ = Number of moles of solute

    n₁ = Number of moles of solvent

Now,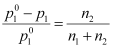             

For dilute solution, n₁ >> n₂

Therefore,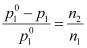             

Or,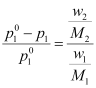                       

Or,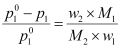                         

Where,        w₂ = Mass of solute

M₂ = Molar mass of solute

w₁ = Mass of solvent

M₁= Molar mass of solvent

Elevation of Boiling Point

• With addition of non-volatile solute, vapour pressure decreases and hence, boiling point increases.

Here,            = Elevation of boiling point

Where,

T_b = Boiling of solution

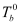= Boiling point of solvent

    ΔT_b ∝ m (for dilute solution)

⇒ ΔT_b = K_bm

Where,        m = Molality

K_b = Proportionality constant known as Boiling Point Elevation Constant or Molal Elevation Constant or Ebullioscopic constant (Unit = K kg mol⁻¹)

However,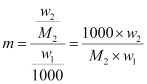   

Where,      w₂ = Mass of solute

M₂ = Molar mass of solute

w₁ = Mass of solvent

Now,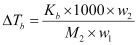         

Or,       

Depression of Freezing point

• With addition of non-volatile solute, vapour pressure decreases, which leads to a decrease in freezing point.

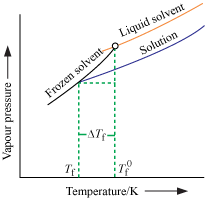
Here, 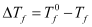= Depression of freezing point

Where, 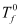       = Freezing point of solvent

T_f = Freezing point of solution

For dilute solution (ideal solution),

ΔT_f   ∝  m

⇒        ΔT_f = K_f m

Where,         m = Molality

K_f = Proportionality constant known as Freezing Point Constant or Molal Depression Constant or Cryoscopic constant (Unit = K kg mol⁻¹)

However,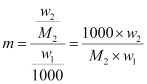     

Where,        w₂ = Mass of solute

M₂ = Molar mass of solute

w₁ = Mass of solvent

Now,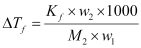         

Or,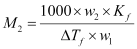             

The value of K_b and K_f can be determined by the following relations:

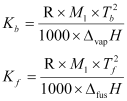
Where,     M₁ = Molar mass of the solvent

       R = Gas constant

       Δ_vapH = Enthalpy of vaporisation

       Δ_fusH = Enthalpy of fusion

Osmosis and Osmotic Pressure

• The process of flow of solvent molecules from pure solvent to solution or from solution of lower concentration to solution of higher concentration through a semi-permeable membrane is called osmosis.
• The pressure required to just stop the flow of solvent due to osmosis is called osmotic pressure (π) of the solution.

• The osmotic pressureπ has to be applied to the solution to prevent osmosis.

• For dilute solution, osmotic pressure is directly proportional to the molarity C of the solution at a given temperature T.

That is,             π = CRT (R = Gas constant)

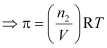
Where,            n₂ = Number of moles of solute

      V= Volume of the solution in litres

Again,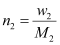           

Where,          w₂ = Mass of the solute

  M₂ = Molar mass of the solute

Now,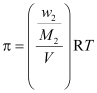             

Or,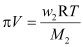       

Or,       

Now, osmosis does not occur between two isotonic solutions.

Isotonic solutions − Solutions having same concentration of solute These solutions have same osmotic pressure.

Hypotonic solution − Solution having a low concentration of solute relative to another.

Hypertonic solution − Solution having a high concentration of solute relative to another.

Reverse Osmosis and Water purification

• If the pressure applied on the solution is greater than its osmotic pressure, then the direction of osmosis is reversed i.e., the solvent starts passing from solution to solvent. The phenomenon is called reverse osmosis.
• This phenomenon is used in purification (desalination) of sea water.