4 Errors in Calculations

Error of a Sum or a Difference

A, B = Two physical quantities

A ± ΔA = Measured value of A

B ± ΔB = Measured value of B

We have to find the error ΔZ in the sum,

Z = A + B

Or Z ± ΔZ = (A ± ΔA) + (B ± ΔB)

The maximum possible error in Z,

ΔZ = ΔA + ΔB

For the difference, Z = A − B, we have

Z ± ΔZ = (A ± ΔA) − (B ± ΔB)

= (A − B) ± ΔA ± ΔB

± ΔZ = ± ΔA ± ΔB

The maximum possible value of error in Z,

ΔZ = ΔA + ΔB

Rule: When two quantities are added or subtracted, the absolute error in the final result is the sum of the absolute errors in the individual quantities.

Error of a Product or a Quotient

Suppose Z = AB, and the measured values of A and B are A ± ΔA and B ± ΔB respectively. Then, Z ± ΔZ = (A ± ΔA) (B ± ΔB)

Z ± ΔZ = AB ± BΔA ± AΔB ± ΔAΔB

Dividing LHS by Z and RHS by AB, we have,

1 ± (ΔZ/Z) = 1 ± (ΔA/A) ± (ΔB/B) ±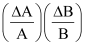

Since ΔA and ΔB are small, we shall ignore their product.

Maximum relative error,

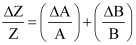
This is true for division as well.

Error in the Case of a Measured Quantity Raised to a Power

Suppose Z = A²

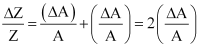
Then, 

Hence, the relative error in A² is two times the error in A.

In general, if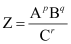

Then,