6 Rounding Off the Uncertain Digits and Determining Uncertainty
Rounding Off the Uncertain Digits and Determining Uncertainty
Rule 1
If the digit to be dropped is less than 5, then the preceding digit is left unchanged.
Example:Â 9.83 is rounded off to 9.8
Rule 2
If the digit to be dropped is more than 5, then the preceding digit is raised by one.
Example:Â 6.38 is rounded off to 6.4
Rule 3
If the digit to be dropped is 5, followed by a non-zero digit, then the preceding digit is raised by one.
Example:Â 14.252 is rounded off to 14.3
Rule 4
If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit (if even) is left unchanged.
Example:Â 6.250 becomes 6.2 on rounding off
Rule 5
If the digit to be dropped is 5 or 5 followed by zeros, then the preceding digit (if odd) is raised by one.
Example:Â 9.750 is rounded off to 9.8
Rules for Determining the Uncertainty in the Results of Arithmetic Calculation
Rule 1
Example:
The length and breadth of a thin rectangular sheet, measured using a metre scale, are 18.2 cm and 14.5 cm respectively. Find the uncertainty or error in the estimation of the area of the rectangular sheet.
Solution:
There are three significant figures in each measurement. This means that the length, l may be written as
l = 18.2 ± 0.1 cm
= 18.2 cm ± 0.5%
Similarly, the breadth, b may be written as
b = 14.5 ± 0.1 cm
= 14.5 cm ± 0.7%
Then, the error of the product, using the combination of errors rule
lb = 263.9 cm2 ± 1.2%
The final result will be
lb = 264 ± 1%
(
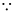As per the rule, the final value of area can contain only 3 significant figures and the error can contain only 1 significant figure.)
Rule 2
If a set of experimental data is specified to n significant figures, the result obtained by combining the data will be valid to n significant figures.
However, if the data are subtracted, the number of significant figures would reduce.
Example: (13.9 g − 6.06 g) both specified to three significant figures gives 7.84 g.
But in addition and subtraction, the final result should retain as many decimal places as there are in the number with the least number of decimal places. So, the answer would be 7.8 g.
Rule 3
The relative error of a value of number specified to significant figures depends not only on ‘n’ but also on the number itself.
Example:
Suppose
m1 = (1.02 ± 0.1 kg), and
m2 = (9.32 ± 0.01 kg)
Both the measured masses have an error or uncertainty of 0.01 kg.
The relative error in 1.02 kg is
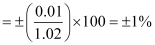
Similarly, the relative error in 9.32 kg is
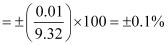
Thus, the relative error depends on the number itself.
Rule 4
In a multi-step computation, the intermediate results in each measurement should be calculated to a significant figure that is one more than the number of digit in the least precise measurement.