7 Dimensions of Physical Quantities and Its Applications

Dimensions of Physical Quantities and Its Applications

• Dimensions

They are the powers (or exponents) to which the units of base quantities are raised for representing a derived unit of that quantity.

Examples: Dimensional formula of volume [M⁰L³T⁰]

Dimensional formula of velocity [M⁰LT⁻¹]

Dimensional formula of acceleration [M⁰LT⁻²]

• Applications of Dimensional Analysis

• Checking the dimensional consistency of equations
• Deducing relation among the physical quantities.

• Checking the Dimensional Consistency of Equations

Based on the principle of homogeneity of dimensions

• According to this principle, only that formula is correct in which the dimensions of the various terms on one side of the relation are equal to the respective dimensions of these terms on the other side of the relation.
• Example:

Check the correctness of the relation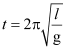, where l is length and t is time period of a simple pendulum; g is acceleration due to gravity.

Solution:

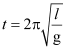
Dimension of L.H.S = t = [T]

Dimension of R.H.S =

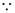(2π is a constant)

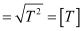
Dimensionally, L.H.S = R.H.S; therefore, the given relation is correct.

• Deducing Relation Among Various Physical Quantities

Based on the principle of homogeneity of dimensions

• Example:

The centripetal force, F acting on a particle moving uniformly in a circle may depend upon the mass (m), velocity (v) and radius (r) of the circle. Derive the formula for F using the method of dimensions.

Solution:

Let F = km^av^br^c … (i)

Where, k is the dimensionless constant of proportionality, and a, b, c are the powers of m, v, r respectively.

On writing the dimensions of various quantities in (i), we get

[M¹L¹T⁻²] = M^a [LT⁻¹]^b L^c

= M^aL^bT^−bL^c

M¹L¹T⁻² = M^aL^b + cT^−b

On applying the principle of homogeneity of dimensions, we get

a = 1,

b= 2,

b + c = 1 …(ii)

From (ii), c = 1 − b = 1 − 2 = −1

On putting these values in (i), we get

F = km¹v²r⁻¹

OR

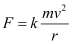
This is the required relation for centripetal force.