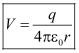1 Electrostatic Potential Energy _ Electrostatic Potential

Electrostatic Potential Energy & Electrostatic Potential

• Change in electric potential energy of a system of charges is defined as the negative of the work done by the electric forces as the configuration of the system is changed.
• Let us consider a system of two charges q₁ & q₂, separated by a certain distance. Suppose that q₁ is fixed at A and q₂ is gradually moved away from its initial position B towards C; as shown in the diagram below:

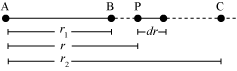
On its way towards C, let us consider an arbitrary point P when the charge q₂ is at a distance r from A, and then a small displacement dr from P.

Force on q₂ when it is at P is,

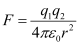,  along AB.

The work done by this force in the small displacement dr is,

Hence the total work done as the charge q₂ moves from B to C is,

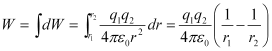
Thus the change in potential energy of this system of charge is,

Now consider the charge q₂ to be brought from infinity to the position P, the potential energy stored in the system of these two charges will be,

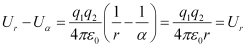
The above equation gives the potential energy of a pair of charges.

• Electric potential at a point P is defined as the change in electric potential energy per unit positive charge when it is brought from a reference point to the point P, in presence of an electric field.

Suppose a unit positive charge is brought from a reference point Q to the point P, and let V_P& V_Qbe the potentials at P and Q respectively, the change in electric potential of the system is,

If the reference point Q is at infinity, we can write,

• Electric potential is also defined as the work done by an external agent on a unit positive charge in moving the test charge form a reference point to a point P, without changing its kinetic energy.

Let W_ext be the work done by the external agent in bringing the unit positive charge from the reference point Q to the point P without changing its kinetic energy, and W_E be the work done by the electric field when the charge was moved. Then from the work-energy theorem the net work done on the charge is zero. Hence, we can write,

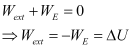
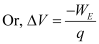
Electric Potential Due to a Point Charge

Let P be the point at a distance ‘r’ from the origin O at which the electric potential due to charge +q is required.

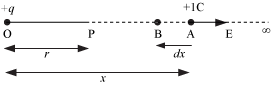
The electric potential at point P is the amount of work done in carrying a unit positive charge from ∞ to P.

Let ‘A’ be an intermediate point on this path, where OA = x. The electrostatic force on unit positive charge is

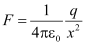, along OA

Small work done in moving through a distance ‘dx’,

∴Total work done in moving unit positive charge from ∞ to point P is

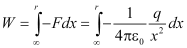
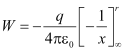
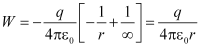
By the definition of potential, this is the potential at P due to the charge at O.