2 Doppler Effect _ Coherent and Incoherent Addition of Waves

Doppler Effect & Coherent and Incoherent Addition of Waves

The Doppler Effect

• We should be careful in constructing the wavefronts, if the source (or observer) is moving.
• If the source moves away from the observer, then wavefronts have to travel a greater distance to reach the observer and hence, will take a longer time.
• Thus, when the source moves away from the observer, the frequency as measured by the source will be smaller. This is known as the Doppler effect.
• The increase in wavelength due to Doppler effect is red shift since a wavelength in the middle of the visible region of the spectrum moves towards the red end of the spectrum.
• When waves received from a source move towards the observer, there is an apparent decrease in wavelength. This is referred to as blue shift.
• The fractional change in frequencyΔν/ν is given by

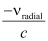
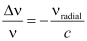
Where,  is component of the source velocity along the line joining the observer to the source relative to the observer

Coherent and Incoherent Addition of Waves

• Coherent sources: Two sources of light emitting light waves of same frequency or wavelength and of a stable phase difference
• Principle of superposition of light waves: When two or more wave trains of light travelling in a medium superpose upon each other, the resultant displacement at any instant is equal to the vector sum of the displacements due to individual waves.

If, 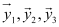… be the displacement due to different waves, then the resultant displacement is given by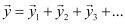

• Conditions for constructive and destructive interference:

Let the displacement of the waves from the sources S₁ and S₂ at point P on the screen at any time ‘t’ be given by,

y₁ = a₁ sin ωt

and

y₂ = a₂ sin (ωt + Φ)

Where, Φ is the constant phase difference between the two waves

By the superposition principle, the resultant displacement at point P is given by,

y = y₁ + y₂

y = a₁ sin ωt + a₂ sin (ωt + Φ)

= a₁ sin ωt + a₂ sin ωt cos Φ + a₂ cos ωt sin Φ

y = (a₁ + a₂ cos Φ) sin ωt + a₂ sin Φ cos ωt …(i)

Let

Then, equation (i) becomes

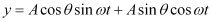
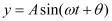
Squaring and adding both sides of the equations (ii) and (iii), we obtain

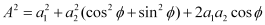
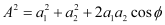
The intensity of light is directly proportional to the square of amplitude of the wave. The intensity of light at point P on the screen is given by,

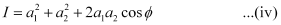
Constructive interference → cos Φ is Maximum i.e., cos Φ = + 1

Φ = 0, 2π, 4π, …

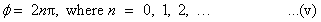
The phase difference Φ between the two waves will be

Where, x is the path difference, using equation (v)

The condition for constructive interference, that is equation (vi), becomes

x = nλ, where n = 0, 1, 2, 3, …

It is the condition for constructive interference between two light waves in terms of path difference between them.

Destructive interference → From equation (iv), it follows that the intensity of light at point P will be minimum, if

Φ = π, 3π, 5π, …

Φ = (2n + 1) π, where n = 0, 1, 2, … (vii)

From equations (vi) and (vii), we have

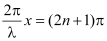
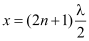, where n = 0, 1, 2, …

This is the condition for destructive interference in terms of phase difference and path difference.