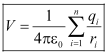3 Equipotential Surfaces _ Potential due to a System of Charges

Equipotential Surfaces & Potential due to a System of Charges

Equipotential Surfaces

An equipotential surface is that surface at every point of which, the electric potential is the same.

We know that,

q(V_B − V_A) = W_AB, q being a test charge.

If points A and B lie on an equipotential surface, then

V_B − V_A = 0

∴ W_AB = q(V_B − V_A) = 0

• No work is done in moving the test charge from one point of equipotential surface to the other.
• For any charge configuration, equipotential surface through a point is normal to the electric field at that point.
• Equipotential surfaces of a single point charge are concentric spherical surfaces centred at the charge.

Potential due to a System of Charges

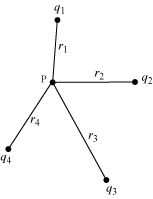
Let there be a number of point charges q₁, q₂, q₃, … q_n at distances r₁, r₂, r₃, … r_n respectively from the point P, where electric potential is to be calculated.

Now, potential at P due to charge q₁,

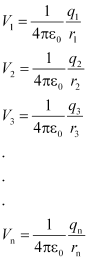
Using superposition principle, we obtain the resultant potential at P due to total charge configuration as the algebraic sum of the potentials due to individual charges.

∴ V = V₁ + V₃ + V₃ + … + V_n

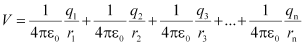
Or,