3 Interference of Light Waves and Young_s Experiment

Interference of Light Waves and Young’s Experiment

• If we use two sodium lamps illuminating two pinholes, then we will not observe any interference fringes.
• The British physicist Thomas Young made two pinholes S₁ and S₂ (very close to each other) on an opaque screen. These were illuminated by another pinhole that was in turn, lit by a bright source. S₁ and S₂ behave similar to two coherent sources because light waves coming out from S₁ and S₂ are derived from the same original source.

• Expression for Fringe Width in Young’s double slit experiment

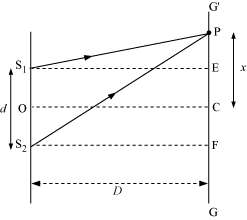
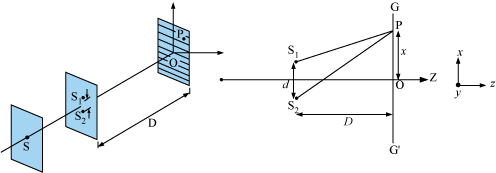
Let S₁ and S₂ be two slits separated by a distance d is the screen at a distance D from the slits S₁S₂. Point C is equidistant from both the slits. The intensity of light will be maximum at this point because the path difference of the waves reaching this point will be zero.

At point P, the path difference between the rays coming from the slits S₁ and S₂ is given by,

Path difference = S₂P – S₁P

Now, S₁ S₂ = d, EF = d, and S₂F= D

∴In ΔS₂PF,

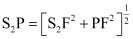
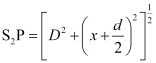
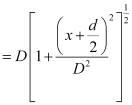
Similarly, in ΔS₁PE,

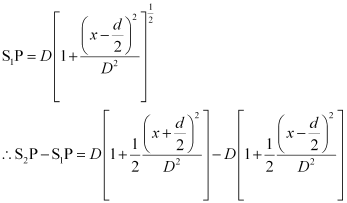
On expanding it binomially,

For bright fringes (constructive interference), the path difference is integral multiple of wavelengths i.e., path difference is nλ.

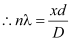
, where n = 0, 1, 2, 3, 4, …

For n = 0, x₀ = 0

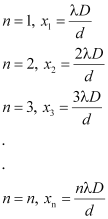
Fringe width (β) → Separation between the centres of two consecutive bright fringes is called the width of a dark fringe.

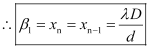
Similarly, for dark fringes,

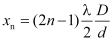
For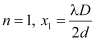

For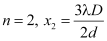

The separation between the centres of two consecutive dark interference fringes is the width of a bright fringe.

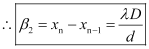
∴β₁ = β₂

All the bright and dark fringes are of equal width as β₁ = β₂

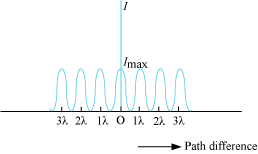
• Graph of intensity distribution in Young’s double slit experiment