4 Diffraction

Diffraction

• Diffraction at a single slit (Fraunhofer diffraction)

The phenomenon of bending of light round the sharp corners of an obstacle and spreading into the regions of the geometrical shadow is called diffraction.

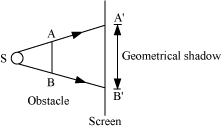
• Expression For Fringe Width

Consider a parallel beam of light from a lens falling on a slit AB. As diffraction occurs, the pattern is focused on the screen XY with the help of lens L₂. We will obtain a diffraction pattern that is a central maximum at the centre O flanked by a number of dark and bright fringes called secondary maxima and minima.

Central Maximum − Each point on the plane wave front AB sends out secondary wavelets in all directions. The waves from points equidistant from the centre C lying on the upper and lower half reach point O with zero path difference and hence, reinforce each other producing maximum intensity at point O.

• Positions and Widths of Secondary Maxima and Minima

Consider a point P on the screen at which wavelets travelling in a direction making angle θ with CO are brought to focus by the lens. The wavelets from points A and B will have a path difference equal to BN.

From the right-angled ΔANB, we have

BN = AB sinθ

BN = a sinθ …(i)

Suppose BN = λ and θ = θ₁

Then, the above equation gives

λ = a sin θ₁

Such a point on the screen will be the position of first secondary minimum.

If BN = 2λ and θ= θ₂, then

2λ = a sin θ₂

Such a point on the screen will be the position of second secondary minimum.

In general, for n^th minimum at point P,

If y_n is the distance of the n^th minimum from the centre of the screen, then from right-angled ΔCOP, we have

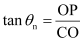
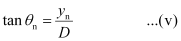
In case θ_n is small, sin θ_n ≈ tan θ_n

∴Equations (iv) and (v) give

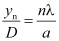
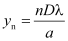
Width of the secondary maximum,

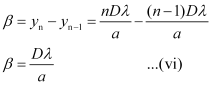
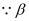is independent of n, all the secondary maxima are of the same width β.

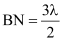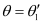If and , then from equation (i), we have

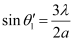
Such a point on the screen will be the position of the first secondary maximum.

Corresponding to path difference,

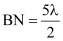and 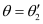, the second secondary maximum is produced

In general, for the n^th maximum at point P,

If 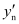is the distance of n^th maximum from the centre of the screen, then the angular position of the n^th maximum is given by,

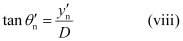
In case 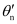is small,

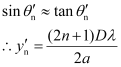
Width of the secondary minimum,

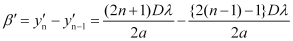
Since 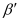is independent of n, all the secondary minima are of the same width.

Resolving Power of Optical Instruments

• Resolving power of a microscope is defined as the reciprocal of the least separation between two close objects, so that they appear just separated when seen through the microscope.

∴Resolving power of microscope,

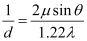
Where,

d → Least distance between the two objects so that their diffraction images are just resolved

θ → Semi-vertical angle of the cone in which rays of light from an object enter the objective of the microscope

μ → Refractive index of the medium

λ → Wavelength of the light used to observe the objects

• Resolving Power of Telescope

Resolving power of a telescope is defined as the reciprocal of the smallest angular separation between two distant objects, so that they appear just separated when seen through the telescope.

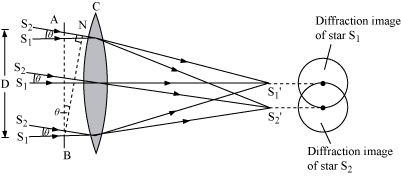
Resolving power of the telescope,

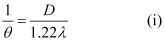
Where,

θ → Angular separation between the two stars

λ → Wavelength of the light in which the two stars are observed

D → Diameter of the objective O of the telescope