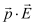4 Potential Energy in an External Field

Potential Energy in an External Field

Potential Energy of a Single Charge

Work done in bringing a charge q from infinity to a point P, in an external field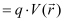

Let,

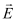= Strength of the external electric field

= External potential at any point P, of position vector

This work done is stored in the charged particle in the form of its potential energy.

∴Potential energy of a single charge q, at distance 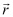, in an external field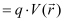

Potential Energy of a System of Two Charges in an External Field

The work done in bringing a charge q₁ from infinity to position 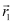is

W₁ =

Now, the work done in bringing a charge q₂ from infinity to position 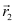, against an external field is

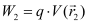
Let,

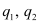= Two point charges at position vectors  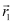and 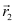 respectively

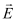= Intensity of the external electric field

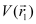= Potential at  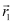due to the external field

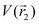= Potential at 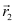due to the external field

For bringing q₂ from infinity to position 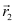, work has to be done against the field due to q₁.

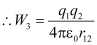
Where, = Distance between q₁ and q₂

Total work done in assembling the charge configuration = Potential energy of the system

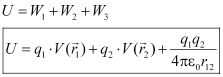
Potential Energy of an Electric Dipole, When Placed in a Uniform Electric Field

Suppose an electric dipole of dipole moment p is placed along a direction, making an angle θwith the direction of an external uniform electric field E. Then, the torque acting on the dipole is given by

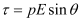
If the dipole is rotated through an infinitesimally small angle dθ, against the torque acting on it, then the small work done is given by

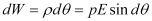
If the dipole is oriented, making an angle θ₁ to θ₂ with the electric filed, then the total work done is given by

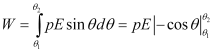
W = pE (cos θ₁ − cos θ₂)

This work done is stored in the dipole in the form of its potential energy.

∴U = pE (cos 90° − cos θ)

U = − pE cos θ

U = −