5 Solenoid and Toroid _ Force Between two Parallel Currents
Solenoid and Toroid & Force Between two Parallel Currents
Solenoid
- It consists of an insulating long wire closely wound in the form of helix.
- Its length is large as compared to its diameter.
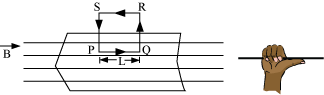
- Magnetic field due to RQ and SP path is zero because they are perpendicular to the axis of solenoid. Since SR is outside the solenoid, the magnetic field is zero.
- The line integral of magnetic field induction
 over the closed path PQRS is
over the closed path PQRS is

From Ampere’s circuital law,
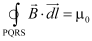 × Total current through rectangle PQRS
× Total current through rectangle PQRS
BL = μ0 × Number of turns in rectangle × Current
BL = μ0nLI
∴ B= μ0nI
Toroid
- It is a hollow circular ring on which a large number of turns of a wire are closely wound.
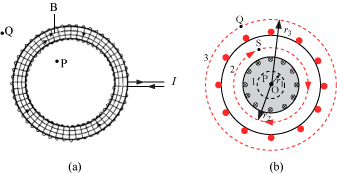
- Three Amperian loops (1, 2, and 3) are shown by dotted lines.
- Magnetic field along loop 1 is zero because the loop encloses no current.
- Magnetic field along loop 3 is zero because the current coming out of the paper is cancelled exactly by the current going out of it.
- Magnetic field at S (along loop 2):
From Ampere’s law,
∴B (2πr) = μ0 NI
Where,
B → Magnetic field
r → Radius
I → Current
N → Number of turns of toroidal coil
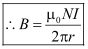
Force between Two Parallel Currents
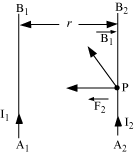
- A1B1 and A2B2 are two infinity long straight conductors.
- I1 and I2 are the current flowing through them and these are r distance apart.
- Magnetic field induction at a point P on conductor A2B2 due to current I1 passing through A1B1 is
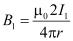
- Unit length of A2B2 will experience a force as
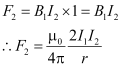
- Conductor A1B1 also experiences the same amount of force, directed towards A2B2. Hence, A1B1 and A2B2 attract each other.
- Two linear parallel conductors carrying currents in the same direction attract each other while in opposite direction repel each other.
Ampere
- One ampere is the current which flows through each of the two parallel uniform long linear conductors, which are placed in free space at a distance of 1 m from each other and which attract or repel each other with a force of 2 × 10−7 N/m of their lengths.
