6 Capacitors and capacitance

Capacitors and capacitance

• A capacitor is a system of two conductors separated by an insulator. The conductors have charges Q and −Q, with potential difference V = V₁− V₂ between them.

• The electric field in the region between the conductors is proportional to the charge Q.
• If potential difference V is the work done per unit positive charge in taking a small test charge from the conductor 2 to 1 against the field, then V is proportional to Q and the ratio Q/Vis a constant:

C =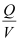

The constant C is called the capacitance of the capacitor.

• Capacitance C depends on shape, size, and separation of the system of two conductors.
• The SI unit of capacitance is Farad.

1 Farad = 1 Coulomb volt⁻¹

The Parallel plate capacitor

• A parallel plate capacitor consists of two large plane parallel conducting plates separated by a small distance.

• Let A be the area of each plate and d the separation between them. The two plates have charges Q and −Q.
• Plate 1 has surface charge density σ = Q/A, and plate 2 has a surface charge density σ.
• Electric field in different regions:

Outer region I,

E =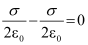

Outer region II,

E =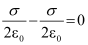

In the inner region between the plates 1 and 2, the electric fields due to the two charged plates add up, giving

E =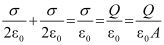

• The direction of electric field is from positive to the negative plate.
• For uniform electric field, potential difference is simply the electric field times the distance between the plates i.e.,

V = E d =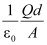

Capacitance C of the parallel platecapacitor is then

Effect of Dielectric on Capacitance

• Consider two large plates, each of area A, separated by a distance d.
• The charge on the plates is ± Q, corresponding to linear charge density ±σ. When there is vacuum between the plates,

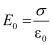
And the potential difference V₀ is

V₀ = E₀d

Capacitance C₀ in this case is

C₀ = Q/ V₀ =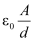

• Consider a dielectric inserted between the plates fully occupying the intervening region. The electric field in the dielectric then corresponds to the case when the net surface charge density on the plates is ± (σ−σ_p ). That is,

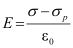
Therefore, the potential difference across the plates is

For linear dielectrics, we expect σ_p to be proportional to E₀ i.e., to σ. Thus, (σ−σ_p ) is proportional to σ and we can write

σ − σ_p =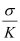

Where, K is a constant characteristic of the dielectric

Clearly, K > 1

Then,

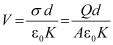
Capacitance C, with dielectric between the plates, is then

C =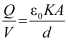

The product ε₀K is called the permittivity of the medium and denoted by ε.

ε = ε₀K