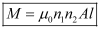6 Inductance
Inductance
Self-induction − Property of a coil by virtue of which the coil opposes any change in the strength of current flowing through it by inducing an emf in itself
Self-induction is also called the inertia of electricity.
• Coefficient of self-induction:
Suppose I = Current flowing in the coil at any time
Φ = Amount of magnetic flux linked
It is found that Φ ∝ I
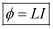
Where,
L is the constant of proportionality and is called coefficient of self induction of the coil
The emf induced in the coil is given by,
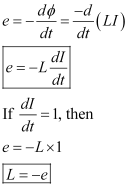
• SI unit of self-inductance is Henry.
• 1 Henry =  = 1 Weber/Ampere
= 1 Weber/Ampere
Self-Inductance of a Long Solenoid
A long solenoid is one whose length is very large as compared to its radius of cross-section. The magnetic field B at any point inside such a solenoid is practically constant and is given by,

Where,
μ0 = Absolute magnetic permeability of free space
N = Total number of turns in the solenoid
∴ Magnetic flux through each turn of the solenoid coil = B × Area of each turn
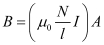
Where,
A = Area of each turn of the solenoid
Total magnetic flux linked with the solenoid
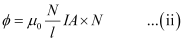
If L is coefficient of self-inductance of the solenoid, then
∴Φ = LI … (iii)
Equating (ii) and (iii),
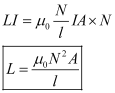
If core is of any other magnetic material, μ0 is replaced by 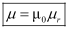
Mutual Induction
The phenomenon according to which an opposing emf is produced in a coil as a result of change in current, hence, the magnetic flux linked with a neighbouring coil is called mutual induction.
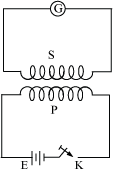
• Coefficient of mutual induction − Consider two coils P and S. Suppose that a current I is flowing through the coil P at any instant i.e.,
Φ ∝ I
Φ = MI … (i)
Where, M is called coefficient of mutual induction
If ‘e’ is the induced emf produced in the S-coil, then
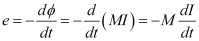
Mutual Inductance of Two Long Solenoids
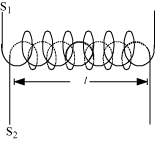
Consider two long solenoids S1 and S2 of same length l, such that solenoid S2 surrounds solenoid S1 completely.
Let
n1 − Number of turns per unit length of S1
n2 − Number of turns per unit length of S2
I1 − Current passed through solenoid S1
Φ21 − Flux linked with S2 due to current flowing through S1
Φ21 ∝ I1
Φ21 = M21I1
Where, M21 is the coefficient of mutual induction of the two solenoids
When current is passed through solenoid S1, an emf is induced in solenoid S2.
Magnetic field produced inside solenoid S1 on passing current through it,
B1 = μ0n1I1
Magnetic flux linked with each turn of solenoid S2 will be equal to B1 times the area of cross-section of solenoid S1.
Magnetic flux linked with each turn of the solenoid S2 = B1A
Therefore, total magnetic flux linked with the solenoid S2,
Φ21 = B1A × n2l = μ0n1I1 × A× n2l
Φ21 = μ0n1n2AI1
∴ M21 = μ0n1n2Al
Similarly, the mutual inductance between the two solenoids, when current is passed through solenoid S2 and induced emf is produced in solenoid S1, is given by
M12 = μ0n1n2Al
∴M12 = M21 = M (say)
Hence, coefficient of mutual induction between the two long solenoids