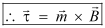6 Torque on Current Loop
Torque on Current Loop
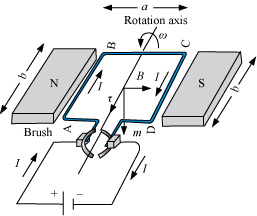
Case I – The rectangular loop is placed such that the uniform magnetic field B is in the plane of loop.
- No force is exerted by the magnetic field on the arms AD and BC.
- Magnetic field exerts a force F1 on arm AB.
∴F1 = IbB
- Magnetic field exerts a force F2 on arm CD.
∴F2 = IbB = F1
Net force on the loop is zero.
- The torque on the loop rotates the loop in anti-clockwise direction.
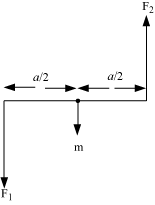
- Torque, τ =
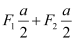
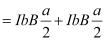
= I(ab)B
τ = IAB
If there are ‘n’ such turns the torque will be nIAB
Where, b → Breadth of the rectangular coil
a → Length of the rectangular coil
A = ab → Area of the coil
Case II – Plane of the loop is not along the magnetic field, but makes angle with it.
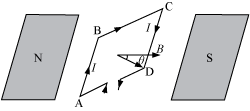
- Angle between the field and the normal is θ.
- Forces on BC and DA are equal and opposite and they cancel each other as they are collinear.
- Force on AB is F1 and force on CD is F2.
F1 = F2 = IbB
- Magnitude of torque on the loop as in the figure:

∴ τ = 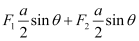
= Iab Bsinθ
τ = IAB sinθ
If there are ‘n’ such turns the torque will be nIAB sinθ
- Magnetic moment of the current, m = IA