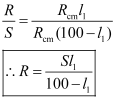7 Kirchhoff_s Rules Wheatstone bridge Meter Bridge

Kirchhoff’s Rules Wheatstone bridge Meter Bridge

Kirchhoff’s First Law − Junction Rule

• The algebraic sum of the currents meeting at a point in an electrical circuit is always zero.

I₁, I₂ I₃, and I₄

Convention:

Current towards the junction − positive

Current away from the junction − negative

I₃ + (− I₁) + (− I₂) + (− I₄) = 0

Kirchhoff’s Second Law − Loop Rule

• In a closed loop, the algebraic sum of the emf is equal to the algebraic sum of the products of the resistances and current flowing through them.

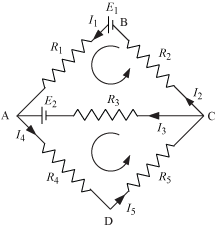
For closed part BACB,

E₁ − E₂ = I₁R₁ + I₂ R₂ − I₃R₃

For closed part CADC,

E₂ = I₃R₃ + I₄R₄ + I₅R₅

• R₁,R₂, R₃, and R₄ are the four resistances.
• Galvanometer (G) has a currentI_g flowing through it at balanced condition,

I_g = 0

• Applying junction rule at B,

∴ I₂ = I₄

• Applying junction rule at D,

∴ I₁ = I₃

• Applying loop rule to closed loop ADBA,

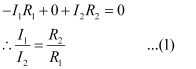
• Applying loop rule to closed loop CBDC,

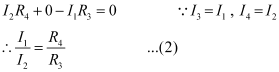
From equations (1) and (2),

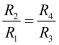(Balanced condition)

• Fora balanced bridge, the unknown resistance can be determined as:

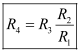
Metre Bridge

• Consists of a 1 m long wire of uniform cross-section
• Construction of the metre bridge is shown in the above figure.

Let

R − Unknown resistance

S − Standard resistance

l₁ − Distance from A

R_cm − Resistance of the wire per unit centimetre

R_cml₁ − Resistance of length AD

R_cm (100 − l₁) − Resistance of length DC

• From the figure, the balance condition gives